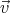 :
: 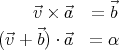
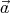 and
and 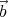 are
constant vectors). Which of these vector fields could be an electrostatic
field?
are
constant vectors). Which of these vector fields could be an electrostatic
field?
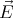 (
(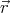 ) = (
) = (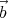 ⋅
⋅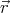 )
)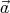
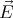 (
(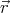 ) =
) = 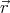
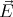 (
(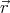 ) = r
) = r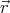
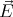 (
(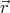 ) =
) = 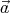 × (
× (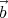 ×
×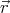 )
)
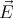 (
(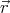 ) = (
) = (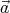 ⋅
⋅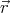 )(
)(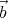 ×
×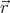 )
)
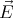 (
(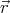 ) =
) = 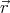 × (
× (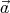 ×
×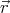 )
)
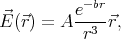
where A and b are constants, and  is the position vector.
is the position vector.
- What is the charge density ρ(
 )?
)?
- What is the total charge?
- Sketch the electric field and potential as a function of the distance from the centre of the sphere.
- What is the total electrostatic energy stored in the sphere?
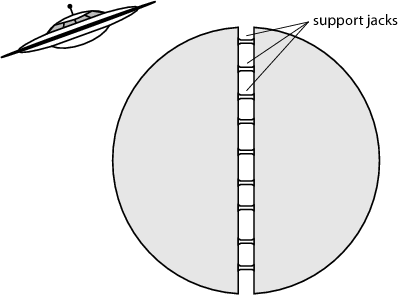
The little green mining engineer was assigned the task to find the force necessary to keep the two halves of the planetoid apart. Help him with the calculations!
(Hint: The equations of the gravitational field are analogous to electrostatics. This problem is equivalent to finding the force needed to keep the two halves of a uniformly charged solid sphere from separating.)