How will change if not the potential of the sphere, but its total charge is kept at a fixed value?
(Note: Based on 4.35 and 4.36 in Griffiths’s book.)
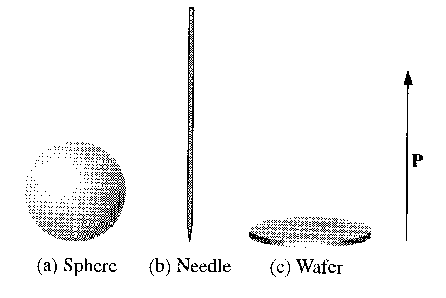
- The cavity is spherical.
- A needle-shaped (long and thin) cavity, parallel to the field.
- A wafer-shaped cavity, perpendicular to the field.
|
|
(Problem 4.16 in Griffiths’s book.)
- Qualitatively describe the motion of a charged particle in this field.
- Find an approximate formula for the drift velocity. Assume that in the region where the particle is moving .