24th of September, 2008

1. Calculate the magnetic field of a current I flowing in a wire when the wire has the following shapes:
   1. an infinitely long straight wire
   2. ring-shaped wire (find the field along the ring’s axis)
   3. a solenoid
2. Show that the monopole term in the expansion of a magnetic field created by a localized steady-state current distribution is always 0.
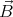3. Prove that if = 0 inside a superconductor, then just above the surface of the superconducting object the normal component of the magnetic field vector is zero.

   A magnetic dipole is levitating above an infinite horizontal superconducting sheet. Use the method of images to find the force on the dipole! If the dipole is free to rotate, what orientation will it adopt?

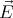4. Find the potential outside an infinitely long metal pipe, of radius R, placed at right angles to an otherwise uniform electric field ₀. Find the surface charge induced on the pipe. (Problem 3.24 from Griffiths.)

   Hint: Use the method of images. Use a “linear dipole” made of two oppositely charged parallel wires, placed very close to each other.

Back to the main page