3rd of September, 2008

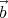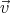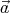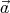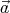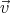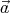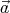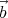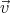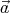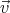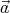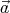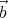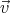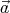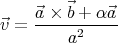
⊥, so ⋅ = 0 and ⋅ = α. Multiplying the first equation by from the left (using the cross product), we get × ( ×) = × ⇔ a² -( ⋅) = ×. Using that ⋅ = α, $⃗a × ⃗b + α ⃗a ⃗v = -----2----- a$
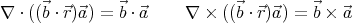
1. $∇ ⋅ ((⃗b ⋅⃗r)⃗a) = ⃗b ⋅⃗a ∇ × ((⃗b ⋅⃗r)⃗a) = ⃗b × ⃗a$
2. $∇ ⋅⃗r = 3 ∇ × ⃗r = 0$
3. $∇ ⋅ (r⃗r) = 4r ∇ × (r⃗r) = 0$
  (Note: The curl of any radially symmetric vector field is 0.)
4. $∇ ⋅ (⃗a × (⃗b × ⃗r)) = - 2⃗a ⋅⃗b ∇ × (⃗a × (⃗b × ⃗r)) = ⃗a × ⃗b$
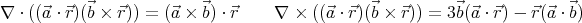
5. $∇ ⋅ ((⃗a ⋅⃗r)(⃗b × ⃗r)) = (⃗a × ⃗b) ⋅⃗r ∇ × ((⃗a ⋅ ⃗r)(⃗b × ⃗r)) = 3⃗b(⃗a ⋅⃗r) - ⃗r (⃗a ⋅⃗b)$
6. $∇ ⋅ (⃗r × (⃗a × ⃗r)) = - 2⃗a ⋅⃗r ∇ ⋅ (⃗r × (⃗a × ⃗r)) = 3⃗r × ⃗a$
The curl of an electrostatic field is 0, so if 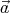and 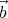are not parallel, then only the fields in points (b) and (c) may be electrostatic fields.
1. The charge density is
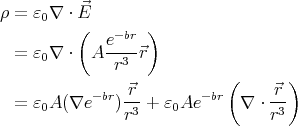
  $ρ = ε0∇ ⋅E⃗ ( -br ) = ε ∇ ⋅ A e---⃗r 0 r3 ⃗r ( ⃗r ) = ε0A(∇e - br)-- + ε0Ae -br ∇ ⋅ -- r3 r3$
  
  Let us calculate the two terms of this sum separately:
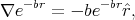
  $-br -br ∇e = - be ˆr,$
  where 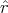= 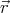∕r, and
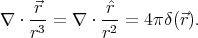
  $∇ ⋅ ⃗r- = ∇ ⋅ ˆr- = 4π δ(⃗r ). r3 r2$
  Thus the complete charge density is
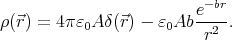
  $-br e--- ρ(⃗r) = 4πε0A δ(⃗r) - ε0Ab r2 .$
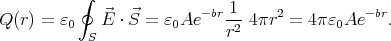
2. The total charge enclosed by a spherical surface S of radius r centred around the origin is $∮ ⃗ ⃗ - br-1 2 -br Q (r) = ε0 S E ⋅S = ε0Ae r2 4πr = 4πε0Ae .$
  Thus as r →∞, the total charge enclosed by the surface goes to 0.
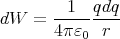
The work needed to add another layer of charge dq to a sphere of radius r and total charge q is $1 qdq dW = 4πε---r-- 0$
The sphere has a homogeneous charge distribution, so q = 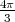r³ρ and dq = 4πρr²dr.
Thus the energy needed to assemble a charged sphere of radius R and charge Q is
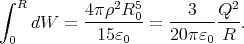
$∫ R 2 5 2 dW = 4πρ-R-0-= --3---Q-. 0 15 ε0 20πε0 R$

Figure 1: The potential and electric field as a function of the distance from the centre of the sphere.

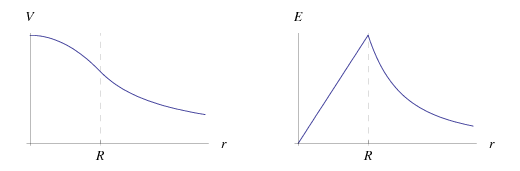
The electric field is
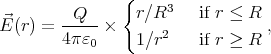${ Q r∕R3 if r ≤ R ⃗E(r) = ----- × , 4 πε0 1∕r2 if r ≥ R$

and the potential is
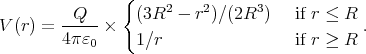${ 2 2 3 --Q-- (3R - r )∕(2R ) if r ≤ R V(r) = 4 πε0 × 1∕r if r ≥ R .$
Let us find the gravitational potential energy W(x) of the two half-spheres as a function of their separation x. The force keeping them together is simply F = dW∕dx.
Creating a gap by separating the halves is equivalent to removing (“mining out”) all the matter from the gap, and distributing it on the surface (i.e. it causes the same change ΔW in energy). Provided that the gap between the halves is very narrow compared to the planet’s radius (x ≪ R), the change in the gravitational field is negligible.
Using Gauß’s law, it is easily shown that the gravitational potential below the surface of the spherical planet is
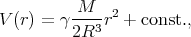
$M--- 2 V(r) = γ 2R3 r + const.,$
where γ is the gravitational constant, M is the mass of the planet, and r is the distance from the centre.
When moving a piece of mass dm up to the surface, the increase in energy is V (R) - V (r)dm. To get the total change in energy, we must integrate over the volume of the gap:
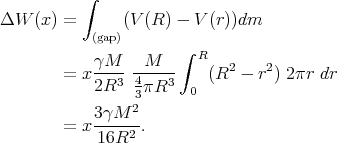$∫ ΔW (x) = (V (R ) - V (r))dm (gap) γM M ∫ R = x---3 4---3- (R2 - r2) 2πr dr 2R 3πR 0 3γM 2 = x-----2 . 16R$ (1)

The force keeping the halves together is
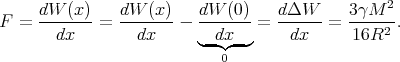
$2 dW--(x) dW-(x)- dW--(0) dΔW--- 3γM--- F = dx = dx - -dx -- = dx = 16R2 . ◟ ◝0◜ ◞$
(I.e. the same as the weight of an object of mass 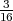M on the surface of the planetoid.)

Back to the main page