10th of September, 2008

1. The electric potential ϕ must satisfy Poisson’s equation.

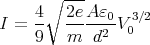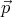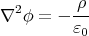
   The spatial charge density can be expressed in terms of the concentration n and charge q of positive and negative ions:

   

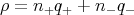
   For simplicity, consider the case when q₊ = -q_- = q, and the concentration of both kinds of ions is n₀ far from the colloidal particle.

   

   For kT ≫ qϕ the approximation e^x ≈ 1 + x can be used. Thus

   

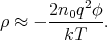
   Substituting this into Poisson’s equation and using the spherical symmetry of the problem we get

   

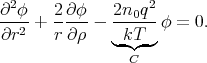
   This differential equation can be written as

   

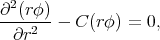
   whose general solution is rϕ = C₁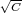e^-r + C ₂e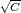^r. For the potential to be zero at infinity, it is required that C₂ = 0. When r → 0, the potential must be the same as in the absence of any ions: C₁ = Q∕4πε₀, where Q is the charge of the colloidal particle.

   

2. The problem can be solved using the method of images. The electric potential inside a conductor is constant, and the field vector near a conducting surface is always perpendicular to the surface. The charges inside the conducting sheet redistribute themselves in such a way that the field created by them balances that component of the dipole’s field which is parallel to the sheet.

   ---

   Figure 1: Using the method of images: the electric field in the right half-space will be the same as a field that would be created by the mirrored dipole ′.

   ---

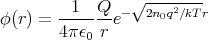
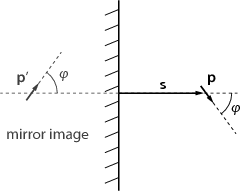
   Let us imagine that the sheet is removed, and another electric dipole 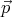′ is added in such a way that it is the mirror image of 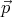with respect to the plane of the sheet, but its direction is reversed (see figure 1). It is easy to see that the electric potential created by 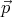and 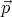′ together is constant in the mirror plane. We know that the solution of Laplace’s equation is unique if the boundary conditions are fixed. Thus the field created in the right-hand-side half-space by the charges on the conducting sheet must be the same as the field created by a mirror dipole 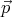′ in the absence of the sheet. Now all we need to do is find the torque acting on 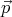in such a field.

   The electric potential created by a dipole 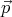′ is

   

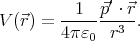
   The electric field vector is

   

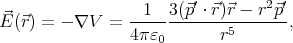
   and the potential energy of a dipole 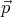in this field is

   

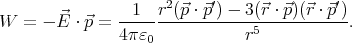
   Let θ and θ′ denote the angles between 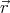, and the vectors 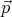and 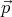’, respectively. If both 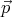and 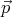′ have the same magnitude, then the potential energy can be written as

   

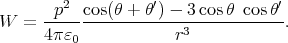
   The magnitude of the torque acting on the dipole 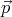is just

   

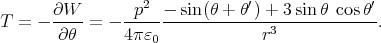
   Let us apply this result to the dipole and its mirror image. We have r = 2s and θ = θ′ = φ, so

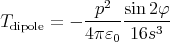   If the dipole is free to rotate, it will adopt one of the positions where the torque is 0, i.e. φ = 0, φ = π∕2, or φ = π. Of these three, φ = π∕2 is an unstable equilibrium, so the dipole will be perpendicular to the plane.

3. We have essentially a one dimensional problem, because A ≫ d. We can write Poisson’s equation for V :

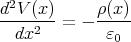
   In a steady state the current density I∕A = ρ(x)v(x) between the plates is constant. Here v(x) denotes the velocity of the electrons when they are at distance x from the cathode. The electrons gain their kinetic energy from the electric field, so E_kinetic = mv²∕2 = eV (x), where e is the elementary charge. Using these two relations we find that ρ(x) = (I∕A)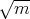∕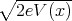. Substituting this result into Poisson’s equation,

   

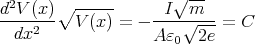
   Note that C > 0 because the physical current is flowing from the anode to the cathode: j < 0. We seek the solution of this differential equation in the form V (x) = βx^α. Substituting this back into the equation we find that α = 4∕3 and β = (9C∕4)^2∕3. This is not a general solution as it does not contain any arbitrary constants but it satisfies the boundary conditions of the problem: V (0) = 0 and 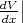_x=0 = 0 (the electric field is 0 at the cathode), so we need seek no further. The final results are

   
   
   

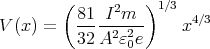
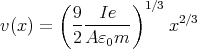
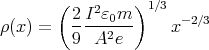
   Putting x = d to find V ₀, we get

   

Back to the main page