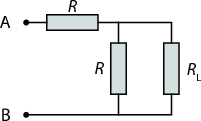Let us divide the cylinder into thin cylindrical shells. A shell of radius r will have a surface current density K = ρωrdr. To find the magnetic field of such a shell, imagine that we bend it into a torus with perimeter p. In the limit p →∞ the torus is an infinitely long cylindrical shell, and we do not need to distinguish between its inner and outer perimeters. Using Ampère’s law and integrating along the “centre ring” of the torus we find that B = μ0K inside the torus. This also holds for a straight cylindrical shell. Outside B = 0.
Summing up the contributions of the shells we find that the magnetic field at distance r from the axis of the cylinder is
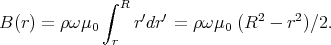
 is
is
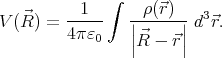
For simplicity let us consider 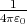 ≡ 1 below.
≡ 1 below.
Let the components of vectors 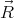 and
and 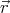 be denoted
be denoted
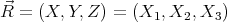
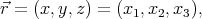
and let F(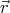 ) = 1∕
) = 1∕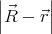 . Now let us expand F(
. Now let us expand F(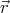 ) in Taylor series, and
write the potential as
) in Taylor series, and
write the potential as
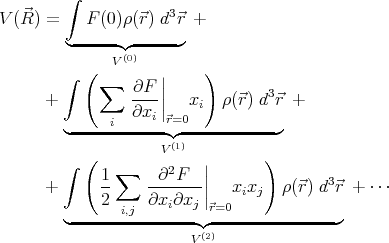 | (1) |
Here V (0) is the monopole term in the expansion of the potential, V (1) is the dipole term, V (2) the quadrupole, etc.
Let us define A, Ai, Aij, … in the following way:
 | = F(0) | ||
 | = 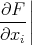  =0 =0 | ||
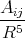 | = 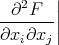  =0 =0 | ||
| … |
| V (0) | = 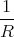 A∫
ρ( A∫
ρ(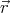 ) d3 ) d3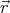 | ||
| V (1) | = 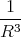 ∑
iAi ∫
xiρ( ∑
iAi ∫
xiρ(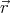 ) d3 ) d3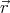 | ||
| V (2) | = 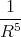 ∑
i,j ∑
i,j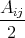 ∫
xixjρ( ∫
xixjρ( ) d3 ) d3 | ||
| … |
Note that the coefficients A, Ai, … only depend on 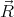 , but not
, but not 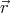 . If we carried
out the tedious calculations, for the first few A-constants we would get
A = 1, Ai = Xi, Aij = 3XiXj - δijR2, where δ
ij is the Kronecker
delta.
. If we carried
out the tedious calculations, for the first few A-constants we would get
A = 1, Ai = Xi, Aij = 3XiXj - δijR2, where δ
ij is the Kronecker
delta.
The monopole term in the potential is just proportional to the total charge
∫
ρ(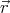 ) d3
) d3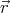 = Q, and does not depend on
= Q, and does not depend on 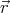 , hence it does not depend on the
choice of origin of our coordinate system. What happens to the dipole term
if the origin of the coordinate system is changed, or, equivalently, the
charges are shifted by a vector
, hence it does not depend on the
choice of origin of our coordinate system. What happens to the dipole term
if the origin of the coordinate system is changed, or, equivalently, the
charges are shifted by a vector 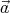 = (a1,a2,a3)?
= (a1,a2,a3)?
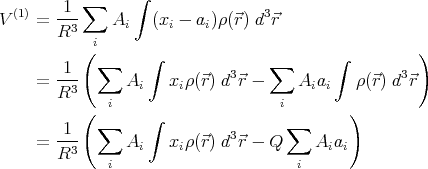 |
Note that if the total charge (and the monopole term in the potential) is 0, then V (1) does not change when the charges are shifted.
Now suppose that V (1) = 0 for any 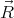 , and thus ∫ x
iρ(
, and thus ∫ x
iρ(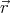 ) d3
) d3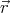 = 0 for each i.
When the charges are shifted, V (2) will be
= 0 for each i.
When the charges are shifted, V (2) will be
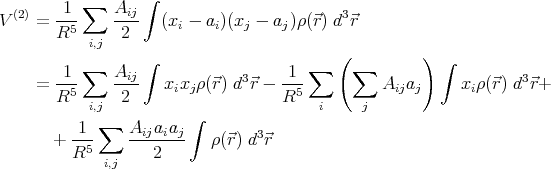 |
Here we used the fact that Aij = Aji to simplify the result. Note again that
if ∫
ρ(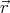 ) d3
) d3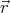 = 0 and ∫ x
iρ(
= 0 and ∫ x
iρ(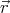 ) d3
) d3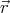 = 0, then V (2) does not change when
shifting the charges.
= 0, then V (2) does not change when
shifting the charges.
It can be shown in a similar way that any V (n) will be independent of the
choice of origin of the coordinate system if V (i) = 0 for all i < n and all
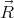 .
.
Adding one more “step” to the infinite ladder will not change it. Let RL denote the resistance of the ladder.
|
|
The configuration of figure 1 must have resistance RL too:
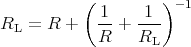
The positive solution of this equation is
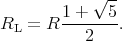
Similarly, if a current I is flowing out from point B, the voltage drop across resistor AB is U2 = RI∕4.
According to the principle of superposition, when we have both a current I flowing into point A and a current I flowing out from point B, the voltage drop across AB will be Utotal = U1 + U2 = 2 ×RI∕4. The resistance between points A and B is Utotal∕I = R∕2.
- Using Gauß’s law we find the electric field at distance r from a
wire E = 1∕2πε0 λ∕r (λ is the linear charge density). The force
on unit length ds of the other wire is
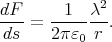
- The moving wires have a current I = vλ. It is easy to find the
magnetic field using Ampère’s law (integrate along circular loops
around the wire): B = μ0∕2π vλ∕r. The force due to the magnetic
interaction is attractive, so the total force is
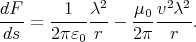
The results in points (a) and (b) are not identical. However, the two presented situations are exactly the same setup, viewed from different reference frames.
This is a good illustration of Maxwell’s equations not being invariant to the
classical Galilei–transformation (x′ = x - vt; t′ = t). If we take
into account the change in charge density due to the relativistic
Lorentz–contraction, λ′ = λ∕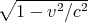 , it is easy to show that
the force is the same in both reference frames. (Use the relation
ε0μ0 = 1∕c2.)
, it is easy to show that
the force is the same in both reference frames. (Use the relation
ε0μ0 = 1∕c2.)