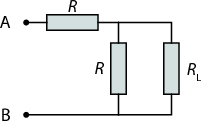24th of September, 2008

1. Let $\rho$ denote the charge density, and $\omega$ the angular velocity.

   Let us divide the cylinder into thin cylindrical shells. A shell of radius $r$ will have a surface current density $K=\rho \omega rdr$. To find the magnetic field of such a shell, imagine that we bend it into a torus with perimeter $p$. In the limit $p\to \infty$ the torus is an infinitely long cylindrical shell, and we do not need to distinguish between its inner and outer perimeters. Using Ampère’s law and integrating along the “centre ring” of the torus we find that $B={\mu }_{0}K$ inside the torus. This also holds for a straight cylindrical shell. Outside $B=0$.

   Summing up the contributions of the shells we find that the magnetic field at distance $r$ from the axis of the cylinder is

   $$B\left(r\right)=\rho \omega {\mu }_0{\int \; <!--nolimits-->}_r^R{r}^{\prime }d{r}^{\prime }=\rho \omega {\mu }_0(R^2-r^2)∕2.$$

2. The potential created by a bounded charge distribution at point $\overrightarrow{R}$ is
   $$V\left(\overrightarrow{R}\right)=\frac{1}{4\pi {\epsilon }_0}\int \; <!--nolimits-->\frac{\rho \left(\overrightarrow{r}\right)}{\left|\overrightarrow{R}-\overrightarrow{r}\right|}{d}^3\overrightarrow{r}.$$

   For simplicity let us consider $\frac{1}{4\pi {\epsilon }_0}\equiv 1$ below.

   Let the components of vectors $\overrightarrow{R}$ and $\overrightarrow{r}$ be denoted

   $$\overrightarrow{R}=(X,Y,Z)=(X_1,X_2,X_3)$$
   $$\overrightarrow{r}=(x,y,z)=(x_1,x_2,x_3),$$

   and let $F\left(\overrightarrow{r}\right)=1∕\left|\overrightarrow{R}-\overrightarrow{r}\right|$. Now let us expand $F\left(\overrightarrow{r}\right)$ in Taylor series, and write the potential as

   $$\begin{array}{cc}\begin{array}{rl}V\left(\overrightarrow{R}\right)& =\underset{V^{\left(0\right)}}{\underbrace{\int \; <!--nolimits-->F\left(0\right)\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}}}+\\ & +\underset{V^{\left(1\right)}}{\underbrace{\int \; <!--nolimits-->\left(\sum _i{\left.\frac{\partial F}{\partial x_i}\right|}_{\overrightarrow{r}=0}{x}_i\right)\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}}}+\\ & +\underset{V^{\left(2\right)}}{\underbrace{\int \; <!--nolimits-->\left(\frac{1}{2}\sum _{i,j}{\left.\frac{{\partial }^{2}F}{\partial x_i\partial x_j}\right|}_{\overrightarrow{r}=0}{x}_i{x}_j\right)\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}}}+\cdots \end{array}& \end{array}$$

   (1)

   Here $V^{\left(0\right)}$ is the monopole term in the expansion of the potential, $V^{\left(1\right)}$ is the dipole term, $V^{\left(2\right)}$ the quadrupole, etc.

   Let us define $A$, $A_i$, $A_{ij}$, … in the following way:

   $$\begin{array}{llll}\hfill \frac{A}{R}& =F\left(0\right)& \hfill & \\ \hfill \frac{A_i}{R^3}& ={\left.\frac{\partial F}{\partial x_i}\right|}_{\overrightarrow{r}=0}& \hfill & \\ \hfill \frac{A_{ij}}{R^5}& ={\left.\frac{{\partial }^{2}F}{\partial x_i\partial x_j}\right|}_{\overrightarrow{r}=0}& \hfill & \\ \hfill \dots & & \hfill \end{array}$$

   Now the terms of the potential’s expansion can be written as

   $$\begin{array}{llll}\hfill V^{\left(0\right)}& =\frac{1}{R}A\int \; <!--nolimits-->\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}& \hfill & \\ \hfill V^{\left(1\right)}& =\frac{1}{R^3}\sum _i{A}_i\int \; <!--nolimits-->x_i\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}& \hfill & \\ \hfill V^{\left(2\right)}& =\frac{1}{R^5}\sum _{i,j}\frac{A_{ij}}{2}\int \; <!--nolimits-->x_i{x}_j\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}& \hfill & \\ \hfill \dots & & \hfill \end{array}$$

   Note that the coefficients $A$, $A_i$, … only depend on $\overrightarrow{R}$, but not $\overrightarrow{r}$. If we carried out the tedious calculations, for the first few $A$-constants we would get $A=1$, $A_i=X_i$, $A_{ij}=3X_i{X}_j-{\delta }_{ij}{R}^2$, where ${\delta }_{ij}$ is the Kronecker delta.

   The monopole term in the potential is just proportional to the total charge $\int \; <!--nolimits-->\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}=Q$, and does not depend on $\overrightarrow{r}$, hence it does not depend on the choice of origin of our coordinate system. What happens to the dipole term if the origin of the coordinate system is changed, or, equivalently, the charges are shifted by a vector $\overrightarrow{a}=(a_1,a_2,a_3)$?

   $$\begin{array}{cc}\begin{array}{rl}{V}^{\left(1\right)}& =\frac{1}{R^3}\sum _i{A}_i\int \; <!--nolimits-->(x_i-a_i)\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}\\ & =\frac{1}{R^3}\left(\sum _i{A}_i\int \; <!--nolimits-->x_i\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}-\sum _i{A}_i{a}_i\int \; <!--nolimits-->\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}\right)\\ & =\frac{1}{R^3}\left(\sum _i{A}_i\int \; <!--nolimits-->x_i\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}-Q\sum _i{A}_i{a}_i\right)\end{array}& \end{array}$$

   Note that if the total charge (and the monopole term in the potential) is 0, then $V^{\left(1\right)}$ does not change when the charges are shifted.

   Now suppose that $V^{\left(1\right)}=0$ for any $\overrightarrow{R}$, and thus $\int \; <!--nolimits-->x_i\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}=0$ for each $i$. When the charges are shifted, $V^{\left(2\right)}$ will be

   $$\begin{array}{cc}\begin{array}{rl}{V}^{\left(2\right)}& =\frac{1}{R^5}\sum _{i,j}\frac{A_{ij}}{2}\int \; <!--nolimits-->(x_i-a_i)(x_j-a_j)\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}\\ & =\frac{1}{R^5}\sum _{i,j}\frac{A_{ij}}{2}\int \; <!--nolimits-->x_i{x}_j\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}-\frac{1}{R^5}\sum _i\left(\sum _j{A}_{ij}{a}_j\right)\int \; <!--nolimits-->x_i\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}+\\ & +\frac{1}{R^5}\sum _{i,j}\frac{A_{ij}{a}_i{a}_j}{2}\int \; <!--nolimits-->\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}\end{array}& \end{array}$$

   Here we used the fact that $A_{ij}=A_{ji}$ to simplify the result. Note again that if $\int \; <!--nolimits-->\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}=0$ and $\int \; <!--nolimits-->x_i\rho \left(\overrightarrow{r}\right)d^3\overrightarrow{r}=0$, then $V^{\left(2\right)}$ does not change when shifting the charges.

   It can be shown in a similar way that any $V^{\left(n\right)}$ will be independent of the choice of origin of the coordinate system if $V^{\left(i\right)}=0$ for all $i<n$ and all $\overrightarrow{R}$.

3. Adding one more “step” to the infinite ladder will not change it. Let $R_L$ denote the resistance of the ladder.

   ---

   Figure 1: Adding one more step to the ladder (represented by $R_L$) does not change its resistance. Thus the resistance between points $A$ and $B$ is $R_L$ as well.

   ---

   The configuration of figure 1 must have resistance $R_L$ too:

   $$R_L=R+{\left(\frac{1}{R}+\frac{1}{R_L}\right)}^{-1}$$

   The positive solution of this equation is

   $$R_L=R\frac{1+\sqrt{5}}{2}.$$

4. If we let a current $I$ flow into point $A$, the current though the resistor between $A$ and $B$ will be $I∕4$ (because of the symmetrical arrangement of the resistors, see fig. 2). Therefore the voltage drop across resistor $AB$ is $U_1=RI∕4$.

   ---

   Figure 2: When current $I$ is flowing into point $A$, the current through resistor $AB$ is $I∕4$.

   ---

   Similarly, if a current $I$ is flowing out from point $B$, the voltage drop across resistor $AB$ is $U_2=RI∕4$.

   According to the principle of superposition, when we have both a current $I$ flowing into point $A$ and a current $I$ flowing out from point $B$, the voltage drop across $AB$ will be $U_{total}=U_1+U_2=2\times RI∕4$. The resistance between points $A$ and $B$ is $U_{total}∕I=R∕2$.

5. Let us calculate the force between the wires in both cases:
   1. Using Gauß’s law we find the electric field at distance $r$ from a wire $E=1∕2\pi {\epsilon }_0\lambda ∕r$ ($\lambda$ is the linear charge density). The force on unit length $ds$ of the other wire is
      $$\frac{dF}{ds}=\frac{1}{2\pi {\epsilon }_0}\frac{{\lambda }^2}{r}.$$

   2. The moving wires have a current $I=v\lambda$. It is easy to find the magnetic field using Ampère’s law (integrate along circular loops around the wire): $B={\mu }_0∕2\pi v\lambda ∕r$. The force due to the magnetic interaction is attractive, so the total force is
      $$\frac{dF}{ds}=\frac{1}{2\pi {\epsilon }_0}\frac{{\lambda }^2}{r}-\frac{{\mu }_0}{2\pi }\frac{v^2{\lambda }^2}{r}.$$

   The results in points (a) and (b) are not identical. However, the two presented situations are exactly the same setup, viewed from different reference frames.

   This is a good illustration of Maxwell’s equations not being invariant to the classical Galilei–transformation ($x^{\prime }=x-vt$; $t^{\prime }=t$). If we take into account the change in charge density due to the relativistic Lorentz–contraction, ${\lambda }^{\prime }=\lambda ∕\sqrt{1-v^2∕c^2}$, it is easy to show that the force is the same in both reference frames. (Use the relation ${\epsilon }_0{\mu }_0=1∕c^2$.)

Back to the main page