- A point charge is in equilibrium if the force acting on it is 0,
i.e. the electric field is zero at the position of the charge.
The equilibrium is stable if when the charge is displaced from the equilibrium position by a small distance, the forces acting on it push it back towards the equilibrium point (and not away from it).
Suppose that there is a stable equilibrium point in a static electric field. The criterion of stability requires that the electric field point inwards on every point of a surface enclosing the equilibrium point. This would mean that the surface integral of the electric field in non-zero on this surface—a result which contradicts that the equilibrium point is in vacuum, i.e. there are no charges inside the surface. Therefore, the original assumption, that there exists a stable equilibrium point, must be false.
- We can use a method similar to that employed in the previous
point. In this case, the force acting on a magnetic dipole is the
negative gradient of its potential energy, i.e.
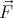 = ∇(
= ∇(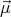 ⋅
⋅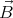 ), where
), where
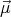 is the dipole moment of the small magnet.
is the dipole moment of the small magnet.
- First, let us take the case when
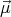 is constant (its orientation
is fixed), and calculate the divergence of
is constant (its orientation
is fixed), and calculate the divergence of 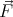 . Choosing the z
axis to be parallel with
. Choosing the z
axis to be parallel with 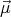 ,
,
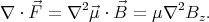
But it can be proven that the Laplcaian of any component of the magnetic field is 0 in vaccum. Taking the curl of both sides of the equation ∇×
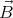 = 0, and using that ∇⋅
= 0, and using that ∇⋅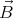 = 0, we
get
= 0, we
get
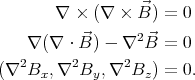
The divergence of
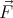 is zero, therefore, in analogy with
the case of the electric field, a small magnet (with fixed
orientation) cannot have a stable equilibrium point in a magnetic
field.
is zero, therefore, in analogy with
the case of the electric field, a small magnet (with fixed
orientation) cannot have a stable equilibrium point in a magnetic
field.
- Now let us take the case when the dipole may rotate freely.
If there is some friction (e.g. the magnet is moving in a
viscuous medium), then, given sufficient time, the magnet will
adopt an orientation that is parallel with the
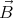 field. Its
potential energy will be Wd = -
field. Its
potential energy will be Wd = -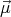 ⋅
⋅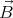 = -μB. In a stable
equilibrium point the potential energy has a minimum. To
simplify the calculations, let us first consider the energy
of a small piece of magnetizable material. Its magnetic
moment is proportional to the magnetic field,
= -μB. In a stable
equilibrium point the potential energy has a minimum. To
simplify the calculations, let us first consider the energy
of a small piece of magnetizable material. Its magnetic
moment is proportional to the magnetic field, 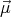 = k
= k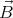 , so
its potential energy is Wm = -kB2. Since W
m can be
obtained from Wd by a monotonous tranformation, for a
positive k, wherever Wm has a minimum, Wd has a minimum
too. So the results obtained for a piece of magnetizable
material (with k > 0) are applicable to a constant magnet
too.
, so
its potential energy is Wm = -kB2. Since W
m can be
obtained from Wd by a monotonous tranformation, for a
positive k, wherever Wm has a minimum, Wd has a minimum
too. So the results obtained for a piece of magnetizable
material (with k > 0) are applicable to a constant magnet
too.
Let us calculate the divergence of the force acting on a piece of magnetizable material:
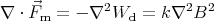
But ∇2B2 can be shown to be positive or zero:
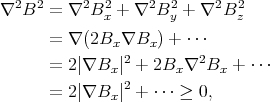
and therefore ∇⋅
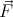 m ≥ 0.
m ≥ 0.
With a reasoning similar to the one used in the previous point it can be shown that a force field having ∇⋅
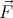 ≥ 0 only has
unstable equilibrium points. (The integral over the Gaussian
surface drawn around the equilibrium point is positive
or zero, therefore there must exist at least some points
on it where
≥ 0 only has
unstable equilibrium points. (The integral over the Gaussian
surface drawn around the equilibrium point is positive
or zero, therefore there must exist at least some points
on it where 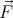 is pointing outwards, or
is pointing outwards, or 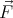 must be zero
everywhere.)
must be zero
everywhere.)
Therefore neihter a small piece of magnetic material with k > 0, nor a little magnet has stable equilibrium points in a static magnetic field. But for a diamagnet k < 0, i.e. the magnetic moment is always oriented antiparallel to
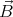 , so a diamagnet does
have stable equilibrium points.
, so a diamagnet does
have stable equilibrium points.
- First, let us take the case when
Let ni denote the index of refraction of the ith layer from the ground, and φi denote the altitude of the star when viewed from that layer. Writing Snell’s law of refraction for the consecutive layers,
| n1 sin(π∕2 - φ1) | = n2 sin(π∕2 - φ2) | ||
| n2 sin(π∕2 - φ2) | = n3 sin(π∕2 - φ3) | ||
| … | |||
| ni sin(π∕2 - φi) | = ni+1 sin(π∕2 - φi+1) | ||
| … |
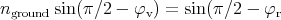 |
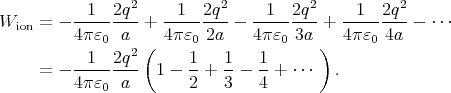 |
The Taylor expansion of ln(1 + x) is
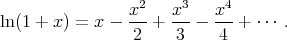
Substituting x = 1 we find that
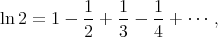
and therefore
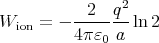
Notice that if we add the energy of all ions in the crystal, we get double the energy of the complete crystal. (If we have only two ions, the energy of the complete system is the energy of one ion in the electric field of the other. Adding the energy of both gives twice this value.) So the electrostatic energy of the crystal per ion is
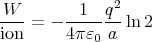
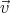 = 0.
Since ∇×
= 0.
Since ∇×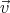 = 0, there exists a scalar field ψ so that
= 0, there exists a scalar field ψ so that 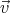 = -∇ψ, and
∇2ψ = 0. This is completely analogous with electrostatics.
= -∇ψ, and
∇2ψ = 0. This is completely analogous with electrostatics.
Now let us examine the problem from the reference frame moving together with the ball. The electrostatic analogy still holds in this reference frame. In this reference frame the ball is not moving, but the water is flowing past the ball. Since the water cannot flow into or out of a solid ball, on the surface of the ball it must be true that
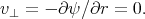 | (A) |
(r is the radial coordinate measured from the centre of the ball.) Very far
from the ball the flow is constant, 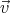 =
= 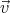 0 (where -v0 is the velocity of the
ball in the original reference frame.)
0 (where -v0 is the velocity of the
ball in the original reference frame.)
How should the homogeneous flow field 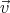 0 be changed so that condition (A)
will be satisfied? We need to find a field
0 be changed so that condition (A)
will be satisfied? We need to find a field 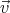 ′ which vanishes at infinity, cancels
the normal component of
′ which vanishes at infinity, cancels
the normal component of 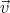 0 on the surface of the sphere, and satisfies
∇⋅
0 on the surface of the sphere, and satisfies
∇⋅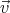 ′ = ∇×
′ = ∇×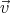 ′ = 0. The sum
′ = 0. The sum 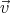 0 +
0 + 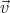 ′ will be the solution.
′ will be the solution.
We have seen a similar problem in electrostatics: a conducting sphere placed in a homogeneous electric field. The difference is that there the tangential (and not normal) component of the electric field needed to be cancelled on the surface of the sphere. There we found that the distortion in the field caused by the sphere is a dipole field.
It turns out that a suitable chosen dipole field can cancel not only the tangential component of a homogeneous field on the surface of a sphere, but the normal component too. A dipole potential has the form
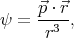
where 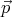 is a constant vector, and the dipole field is
is a constant vector, and the dipole field is
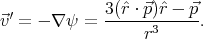
Let us choose 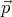 so that it is parallel to
so that it is parallel to 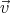 0 and calculate the normal
components of
0 and calculate the normal
components of 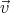 0 and
0 and 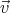 ′ at the surface of the sphere. We shall use spherical
coordinates, with θ being the angle between
′ at the surface of the sphere. We shall use spherical
coordinates, with θ being the angle between 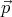 and
and 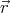 . Let R be the radius of
the sphere.
. Let R be the radius of
the sphere.
| v0⊥ | = 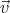 0 ⋅ 0 ⋅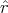 = v0 cos θ = v0 cos θ | ||
| v′⊥ | = 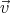 ′⋅ ′⋅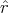 = = 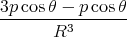 = = 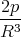 cos θ cos θ |
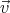 ′ will cancel the normal
component of
′ will cancel the normal
component of 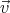 0 on the surface of the sphere. The solution is
0 on the surface of the sphere. The solution is
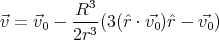
in the reference frame moving together with the ball.