It is known among musicians that when two high pitch tones are played loudly at the same time, a subtle low pitch tone may appear. This is called a combination tone, or a Tartini tone after 18th-century Italian violinist Giuseppe Tartini, who described the effect.

The origin of this phenomenon was debated for a long time among physicists. It was first proposed to be a form of acoustic beats. It was hypothesized by Laplace, Chladni and Young, among others, that when the frequency of the beats becomes high enough, we will perceive them as a separate sound.¹ This theory, however, was not correct. Beats arise from the superposition of independent sounds, and do not contain their frequency difference as an additional component (in the sense of Fourier analysis). What gives rise to the combination tone then? The answer was found only in 1863, when Hermann von Helmholtz suggested that this tone follows from the non-linear transmission in the middle ear.

In this article, I will give a hands-on demonstration of combination tones, along with instructions on how to experiment with them on a computer, and a basic explanation of their origin. But before we proceed, let us listen to the phenomenon!

Combination tones

Important: The sound samples below can be played by clicking the small triangle (play button). Use loudspeakers, not headphones, as the left and right channels of the stereo samples must be heard by both ears simultaneously for the effect to be apparent. Since this is a non-linear effect, turn up the volume.

Listen to these pure tones (sine waves) at 1000 Hz and 1500 Hz, first separately, then together:

1000 Hz   1500 Hz  

1000 Hz and 1500 Hz together, as left and right stereo channels: 

Did you hear the low tone? If not, turn up the volume a bit or lean closer to the speakers. Listen to the tone below to see what pitch to expect, then try again:

Difference tone:  500 Hz  

The pitch of this particular combination tone is the difference of the two frequences, i.e. 500 Hz.²

Many people have difficulty noticing the effect when presented this way. But there is another way, which makes the effect much more obvious: instead of playing two constant pitches, play a constant one and a falling one. Here they are separately:

Steady:   Falling:  

Now let’s listen to them simultaneously. If you listen carefully, you will be able to hear a third tone that is rising. This is the difference tone.

Steady (left) and falling pitch (right): 

Where is it coming from?

Interlude: reproducing the sounds on a computer

If you would like to reproduce this sound on a computer, remember that the phase \(\varphi\) of a wave \(\sin \varphi\) is the time integral of its angular frequency \(\omega = 2\pi f\):

In the example sound above, I produced a tone whose pitch is falling by 100 Hz per second, starting from 1300 Hz. Thus its frequency is changing as \(f = 1300\,\mathrm{Hz} - (100\,\mathrm{Hz/s})\times t\) and its phase is \(\varphi = \int 2\pi f \: dt = 2\pi(1300\, t - 50\, t^2)\).

In Mathematica, the sound can be produced using:

Play[{Sin[2 Pi (1300 t - 50 t^2)], Sin[2 Pi 1500 t]}, {t, 0, 3}]

If you are a MATLAB person, try this:

sr = 22050; % sample rate
time = 0:(1/sr):3;
soundsc([sin(2*pi*(1300*time - 50*time.^2)); sin(2*pi*1500*time)], sr)

If you are a Python fan, run this in a Jupyter notebook:

import numpy as np
from math import pi
from IPython.display import Audio

sr = 22050 # sample rate
time = np.linspace(0, 3, 3*sr)
Audio([np.sin(2*pi*(1300*time - 50*time**2)), np.sin(2*pi*1500*time)], rate=sr)

I am providing this basic code in multiple languages to encourage experimentation. So go ahead and try it now!

The non-linearity of the human ear

Combination tones are created by non-linear transmission in the middle-ear. Let us look at what happens when the sum of two pure tones, \(u(t) = \sin \omega_1 t + \sin \omega_2 t\), is transmitted through a non-linear amplifier.³ Let the function \(a(u)\) describe this amplifier. Since it is non-linear, its series expansion may contain square, cubic and higher order terms as well:

Let us compute the square of the sum of two sine waves. Using the identities

we obtain

Notice that not only the difference but also the sum of the frequencies has appeared. These are one type of combination tone. (The double frequencies \(2x\) and \(2y\) have appeared as well, however these are not very interesting because they coincide with the harmonics.)

The pitches of the sum and difference tones are visualized in green below. The lower one is rising and corresponds to the difference.

Steady (left) and falling pitch (right), 3 seconds: 

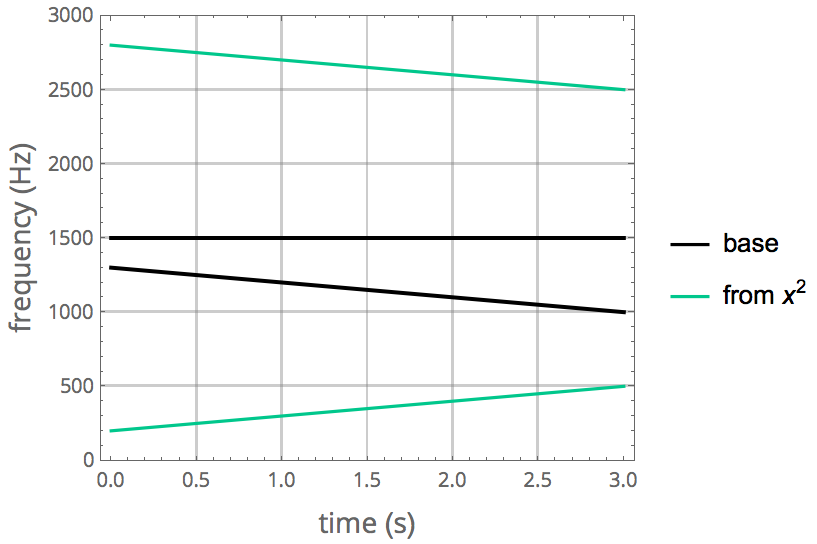
What happens if we now extend the sound sample by a few more seconds and let the second tone fall even further? If you listen carefully, you will hear a new sharply falling tone towards the end:

Steady (left) and falling pitch (right), 5 seconds: 

If you could not hear it, turn up the volume some more. Since this is a non-linear effect, it will be much more prominent at higher volumes. Where is this tone coming from? It is not visible in the plot above. It turns out that it can be explained by the third order term in the expansion of \(a(u)\).

The following plot shows the more interesting second (green) and third (yellow) order combination tones together. The falling yellow line at the bottom is the new tone that we could hear.

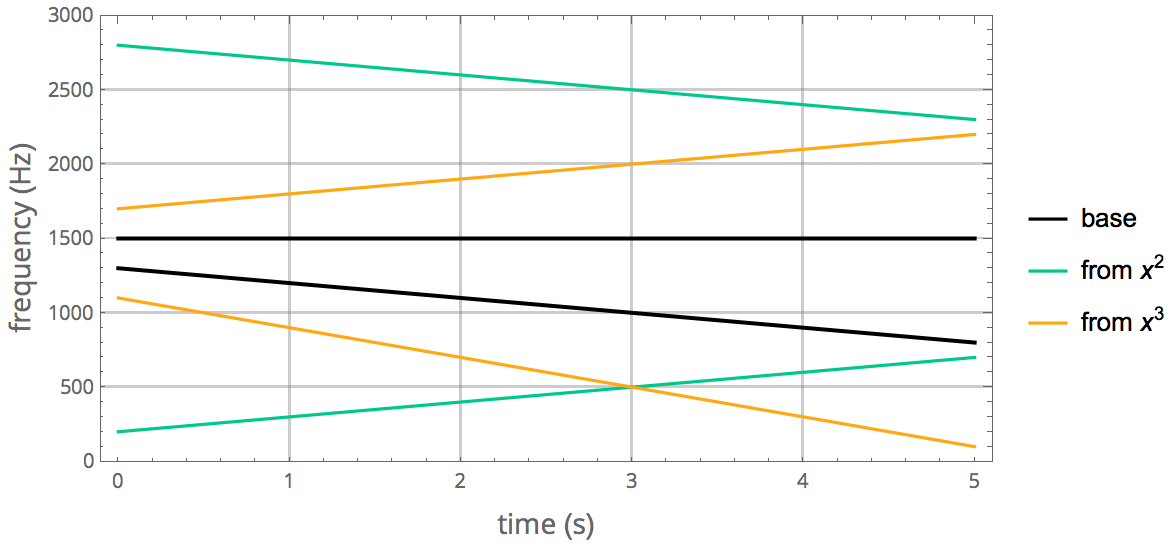
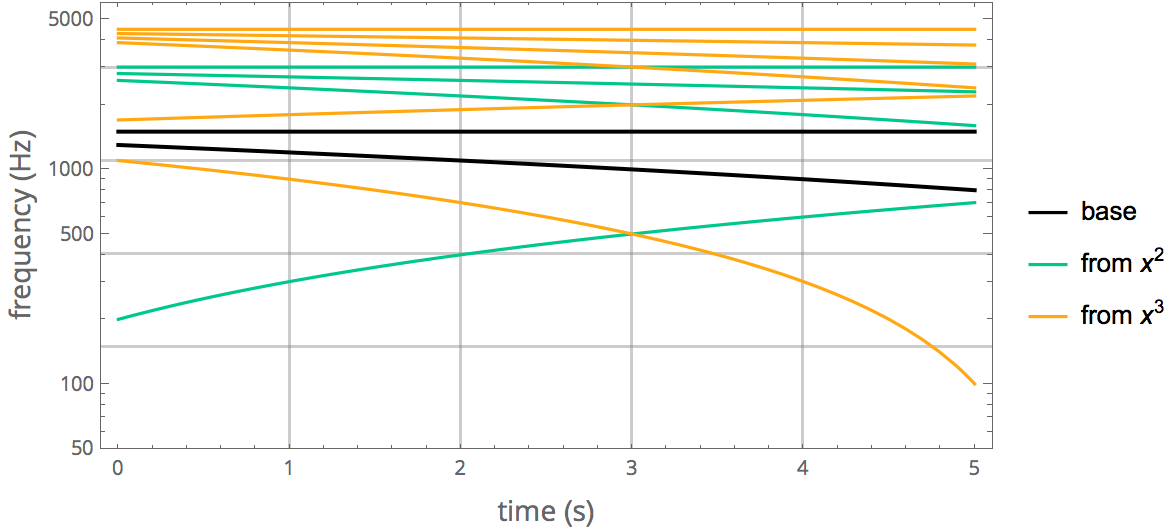
But why does it seem to be falling so much more quickly than the base tone, when we listen to it? This is explained by the logarithmic perception of pitch. Going one step—one musical note—higher in pitch corresponds to a multiplying frequency by a constant. If we plot these tones on a logarithmic scale—now all of them, including the harmonics—the reason for the sharp fall becomes clear. It is this “accelerating” decrease in pitch that draws our attention to this particular combination tone towards the end of the sample.

Revisiting the original example

The first example on this page uses two tones with frequencies of 1000 Hz and 1500 Hz. When I first created this example, I wanted to use musical notes instead. I chose C₆ and G₆, which have frequences \(f_\mathrm{C} = 1046.5\,\textrm{Hz}\) and \(f_\mathrm{G} = 1568.0\,\textrm{Hz}\) in the equally tempered scale. Let us listen these now, and see what we will hear.

G₆   C₆  

C₆ and G₆ together, as left and right stereo channels:  

There is something strange about the difference note now: it appears to wobble. It sounds just like acoustic beats. I can hear about 10 or 11 wobbles in total. Since this is a 3 second sample, that corresponds to a beats frequency of about \(10/3 = 3.33\,\textrm{Hz}\) to \(11/3 = 3.67\,\textrm{Hz}\). Remember that the frequency of the beats is the difference between the frequencies of two similar pitches. Where do the two sounds that create the beats come from?

It turns out that in this case there will be a second and a third order combination tone which are very near in pitch, but not quite equal. Their frequency difference corresponds exactly the to the beats that I could hear:

This is yet another way to demonstrate combination tones. However, to be able to hear this effect clearly, it is important to have just the right level of volume (or keep our ears at just the right distance from the speakers). If the sound is not loud enough, the effect cannot be heard. If the sound is too loud, then higher order combination tones become audible too and change the beats pattern.

If we had used just temperament instead of equal temperament, then the frequency ratio of G and C would have been \(3:2\) exactly. The second and third order combination tones would have coincided and we would not have heard any beats. This is why there are no beats when using 1500 Hz and 1000 Hz tones.

Conclusion

We have learned that passing the sum of two pure sine waves through a non-linear amplifier causes the sum, difference, as well as other integer linear combinations of their frequencies to appear.

This non-linearity can appear in different media that the sound passes through, such as the amplifier in your audio playback equipment. I do not know how strong the non-linearity is in a typical computer’s audio output electronics, but to be on the safe side, all the sound samples above have the two tones separated into the left and right stereo channels. This way the tones may only interact once they leave the loudspeakers. An exception is when the left and right speakers are built into the same housing, as is the case with laptop computers. In this case the non-linearity may be present in the vibration of the laptop body. Indeed, Helmholtz himself was able to observe combination tones in the resonant vibration of membranes.

However, when the experiment is performed with separate speakers, the effect is still clearly audible. In this situation what we are experiencing must indeed be the non-linearity of human ear.

Bonus figure: A spectrogram of the sum of the above steady and falling tones, extended to 8 seconds, and passed through the non-linear amplifier \(a(u) = (\operatorname{sgn} u) \ln(1+|u|)\). We can see the effects of higher than 3rd order terms as well. Created with Sonic Visualizer.